After I had more or less completed the MINC hardware, it soon became clear that the project wasn’t done – it needed a vt105. There was one, a Windows software – but I don’t have Windows, and how that particular software works by adding a layer on top of Telnet wouldn’t easily work with the PDP2011 either. Well maybe it could, I didn’t try.
Instead I took what in my weird style of thinking was ‘the easier way’… I decided to instead take the old terminal core in PDP2011 and make that into a vt105. And, because there’s nothing like doing a proper job, a vt100 and vt102 as well. Based on the same idea: setup the FPGA with an additional PDP11 cpu and some specific hardware to drive a VGA 640×480 screen and interface a PS2 keyboard.
I’ve built the software that runs on the PDP11 cpu for the terminal mostly from scratch – there were relatively few bits of the old terminal core that could be reused, mostly around the keyboard and serial port handling. I took the idea of the escape code parser from the state diagram on vt100.net; although that’s far more complex than really needed for the 7-bit terminal family, it made the code nice and clean – and it can be expanded easily if the need arises.
During development, I used vttest a lot to verify that everything works as it should, and it passes all the tests that I expect it to. But having said that, there are some areas that I’m not sure are bug free yet. Vttest is quite the bag of tricks, but it doesn’t test everything to the same level of paranoia – and I think I might have found that it has an error in its vt100 testing (not sure how to verify that without a real vt100). But, scroll areas remain a bit of a thing, and I should probably redo that code. Not now though.
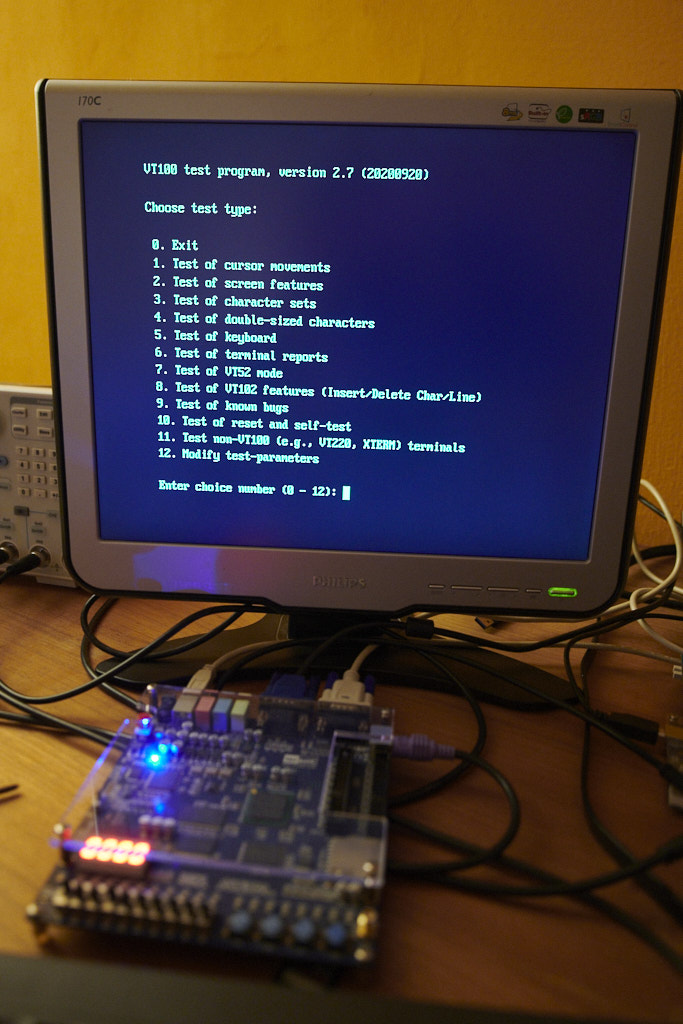
So that’s the vt100 side of things, except that it also does the 3 extras that would make it into a vt102: the DCH, IL and DL escape sequences, and the Insert-Replace mode. And it also does the vt220 DCH sequence. Why? because that makes it a lot easier to live with if you sometimes connect it to a current Linux box as a regular terminal (as I did for running vttest).
And obviously it does everything it needs to make it a vt105 – provided it is configured to do so, because that takes a lot of extra resources from the FPGA. Mainly memories since the latest improvements, but there’s still a marked difference.
That’s where things stand now – except for a number of things that didn’t seem too urgent for the final goal of a MINC+vt105 system. Which is still a pretty long list, and that goes to show how amazing vt100 really was at the time. I’ll include a list below of everything that isn’t implemented yet – that’s quite a bit easier than listing what does work. I’m surprised that the code fits in 8k words actually…
- the 132 column mode; that would be quite complex to do, because it would need a different font, and it wouldn’t really look nice on 640×480 resolution – but changing that too would make the complexity a lot worse again.
- the screen background, ie. dark letters on a bright background. Very easy to do, but I suspect it would look horrible – I never used that back in the day either, it looked horrible on real terminals.
- soft scrolling; not trivial but doable, but I’m not sure I see the point. Again here, back in the day I never used it.
- double height and double width characters; probably a lot of work – and not really necessary for MINC, I think. And there doesn’t seem to be a lot of software that uses it either – at least I can’t think of any.
- hard copy (on a special printer for the real thing but that’s hardly feasible; or instead saving to a bitmap); I’d like to add that at some point. Haven’t really thought how it should work yet.
- keyboard things like setting repeat rate, using the leds for caps lock, num lock and scroll lock – none of that works at this point, the keyboard will repeat but only by its default rate. This should be added in some next version, the main issue is that it needs a change to the ps2 component to allow transmitting commands to the keyboard.
- automatic XON-XOFF. Doesn’t seem an issue, although I do suspect the buffer can be overrun when interfacing to a current Linux system instead of a PDP2011. Should be added in a next version.
- the BREAK signal. Should be added, the only thing there is that I haven’t really figured out how to test it yet.
That’s it – everything else works. If you think the list is long, have a read in the vt105 manual and check out what does work…
Together with this post I’ve also put up the latest version on the download page. Check the new board directories: minc-de10l, that has a complete MINC system with ADC and vt105; and de1vt, which has just a vt100 or vt105 for testing or hooking up to another FPGA board or Linux machine!